坐标系转换技术应用

需求:由两个点A,B组成一个向量，再加一个点C，构成关系，当这两个点转换到另外两个任意位置A'和B'的时候，需要计算C在新的A',B'位置体系中的相对位置

实现原理:

1.将向量AB和C都移动到原点，即起点A到原点

2.将向量A’B’也移动到原点

3.将AB向量旋转到A'B'向量，旋转过程应用到C

4.缩放(模长比值)

5.平移回到A'

原先在第3步旋转过程中，使用Quaternion.FromToRotation函数，发现旋转后的结果对不上，思考原因应该是个两个原点对齐的向量要重叠旋转方式不确定导致，我改用罗德里格斯公式原理，通过分步旋转解决了这个问题，下面具体代码

using UnityEngine;

public class RotationCalculator : MonoBehaviour
{
    #region 原坐标关系
    public Vector3 originStartPos = new Vector3(0.5f, 0.1f, 0.8f);
    public Vector3 originEndPos = new Vector3(3f, 2f, 1f);
    public Vector3 transitionPos = new Vector3(2.5f, 1.5f, 0.8f);
    #endregion

    #region 现坐标关系
    public Vector3 targetStartPos = new Vector3(6f, 2f, 5f);
    public Vector3 targetEndPos = new Vector3(2f, 4f, 5f);
    public Vector3 afterTransitionPos;
    #endregion


    public static Vector3 Transition(Vector3 originStartPos, Vector3 originEndPos, Vector3 transitionPos, Vector3 targetStartPos, Vector3 targetEndPos)
    {
        //1.将要计算的点移动到原点
        var relativePos = transitionPos - originStartPos;
        //2.旋转到目标方向
        var originDir = originEndPos - originStartPos;
        var targetDir = targetEndPos - targetStartPos;
        relativePos = CalcPositionFromDirectionRotate(relativePos, originDir, targetDir);
        //3.缩放
        var scale = Vector3.Magnitude(targetDir) / Vector3.Magnitude(originDir);
        relativePos *= scale;
        //4.平移到目标起点
        var tagetPos = relativePos + targetStartPos;
        return tagetPos;
    }


    /// <summary>
    /// 计算一个相对于方向A的点,当旋转重合到方向B时的位置
    /// </summary>
    /// <param name="pos">要计算的坐标</param>
    /// <param name="fromDir">原方向</param>
    /// <param name="toDir">目标方向</param>
    /// <returns></returns>
    static Vector3 CalcPositionFromDirectionRotate(Vector3 pos, Vector3 originDir, Vector3 targetDir)
    {
        originDir = originDir.normalized;
        targetDir = targetDir.normalized;
        var tempPos = pos;
        #region 1.对齐坐标系(将参考轴重叠到Z轴)
        if (originDir != Vector3.forward)
        {
            var projectXZ_originDir = originDir;
            if (originDir.y != 0)
            {
                //计算originDir在XZ平面上的投影向量
                projectXZ_originDir = Vector3.ProjectOnPlane(originDir, Vector3.up);
            }
            //计算originDir的投影向量与Forward方向在XZ平面的夹角
            var angle_axleY = Vector3.SignedAngle(projectXZ_originDir, Vector3.forward, Vector3.up);
            Debug.LogFormat("绕Y轴旋转:{0}度", angle_axleY);
            //创建绕X轴旋转angle度的四元数
            Quaternion rotationY = Quaternion.AngleAxis(angle_axleY, Vector3.up);
            tempPos = rotationY * tempPos;
            //计算originDir与自己的投影向量在ZY平面的夹角
            var angle_axleX = Vector3.SignedAngle(originDir, projectXZ_originDir, Vector3.right);
            Debug.LogFormat("绕X轴旋转:{0}度", angle_axleX);
            Quaternion rotationX = Quaternion.AngleAxis(angle_axleX, Vector3.right);
            tempPos = rotationX * tempPos;
            Debug.Log("参考轴重叠到Z轴后的坐标位置:" + tempPos);
        }
        #endregion

        #region 2.移动到目标轴(与目标轴对齐)
        if (targetDir != Vector3.forward)
        {
            //计算targetDir在XZ平面上的投影
            var projectXZ_targetDir = targetDir;
            if (targetDir.y != 0) //如果本来就在XZ平向上就不处理
            {
                //在XZ平向的投影
                projectXZ_targetDir = Vector3.ProjectOnPlane(targetDir, Vector3.up);
            }

            //计算Vector3.forward与projectXZ_targetDir在XZ平面的夹角(度)
            float angle_axleY = Vector3.SignedAngle(Vector3.forward, projectXZ_targetDir, Vector3.up);
            Debug.LogFormat("绕Y轴旋转:{0}度", angle_axleY);
            //创建绕Y轴旋转angle度的四元数
            Quaternion rotationY = Quaternion.AngleAxis(angle_axleY, Vector3.up);
            tempPos = rotationY * tempPos;

            if (projectXZ_targetDir != targetDir)
            {
                //计算投影向量与目标向量在zy平向上的夹角
                var angle_axleX = Vector3.SignedAngle(projectXZ_targetDir, targetDir, Vector3.right);
                Debug.LogFormat("绕X轴旋转:{0}度", angle_axleX);
                //创建绕X轴旋转angle度的四元数
                Quaternion rotationX = Quaternion.AngleAxis(angle_axleX, Vector3.right);
                tempPos = rotationX * tempPos;
            }
        }
        #endregion
        return tempPos;
    }



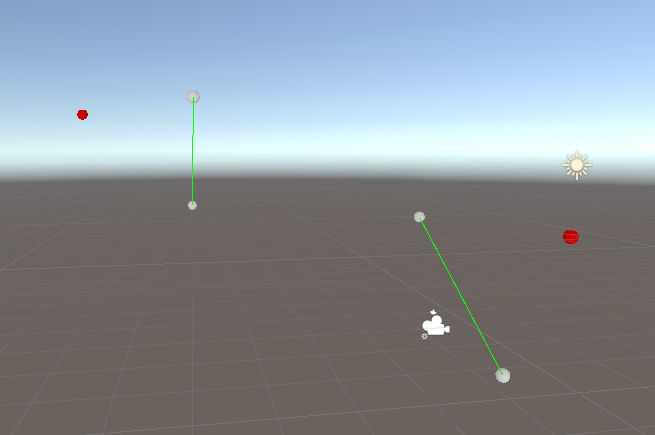
    // 可视化调试
    void OnDrawGizmos()
    {
        Gizmos.color = Color.white;
        Gizmos.DrawSphere(originStartPos, 0.1f);     
        Gizmos.DrawSphere(originEndPos, 0.1f);     

        Gizmos.color = Color.green;
        Gizmos.DrawLine(originStartPos, originEndPos);

        Gizmos.color = Color.red;
        Gizmos.DrawSphere(transitionPos, 0.1f);


        Gizmos.color = Color.white;
        Gizmos.DrawSphere(targetStartPos, 0.1f);
        Gizmos.DrawSphere(targetEndPos, 0.1f);

        Gizmos.color = Color.green;
        Gizmos.DrawLine(targetStartPos, targetEndPos);

        Gizmos.color = Color.red;
        afterTransitionPos = Transition(originStartPos, originEndPos, transitionPos, targetStartPos, targetEndPos);
        Gizmos.DrawSphere(afterTransitionPos, 0.1f);

    }
}

效果图:

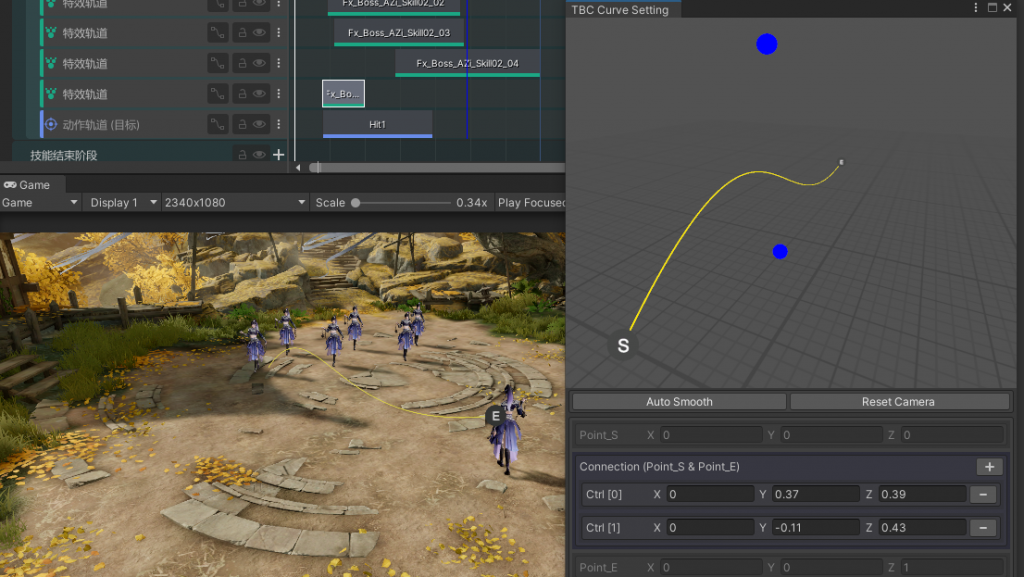
技术应用

在技能编辑器中编辑一个3D的贝塞尔曲线，使用者本质只是编辑出了曲线的走势，所以我在(0,0,0)到(0,0,1)方向让使用者添加控制点，最终会在实际的人物与目标之前换算出这个曲线轨迹

坐标系转换技术应用

文章评论